Mean Paper Aeroplanes

Today we threw paper aeroplanes in my year 7 lessons and it was a lot of fun!
Underlying all the fun, however, was a serious competition and competitions must have winners. To win fairly you probably need to throw more than once to account for variances in skill, luck and craftsmanship. In throwing more than once you introduce a dilemma – how do you choose a winner? This is where I wanted my pupils to get stuck and was the whole reason for mounting the competition in the first place.
Let’s back up a bit to how we got here.
- For homework the night before, pupils watched a video tutorial on how to make a paper aeroplane. They used a template (downloadable below), printed on card, to make their own plane.
- In the lesson, students were given roles before we went across to sports hall. Roles included Thrower, Measurer, Recorder, Retriever and Judge.
- With close-to-military precision, aeroplanes were launched in 4 places simultaneously, each distance measured and then recorded in a Google spreadsheet on the Chromebooks.
- Once everyone had thrown 3 valid throws, we returned to class to decide a method for choosing a winner.
Problem
An average distance is one fair way to select a winner so I could teach them to find the mean, for example, by telling them to add all the numbers and divide by the number of numbers. For me, as a learner and as a teacher, that is unsatisfactory. I want to know why you find the mean that way. It’s certainly not because mean is the meanest of all the averages.
Mirror, Mirror, on the wall! Which is the meanest average of them all?
Perhaps because we’re dealing with multiple concepts at the same time (context, average, sum, division) it’s not an easy one to explain. But if pupils don’t understand why you add then divide, it’s quite likely to be forgotten, confused with the mode or median, or muddled into something completely nonsensical. Surely it’s more robust to really understand why the mean is calculated that way and not just how?
Solution
Using a sequence of minimally different examples, the class led itself to the idea that we needed a fair number to represent each person’s set of throws. In other words, we hit upon needing an average.
Some members of the class already knew about the mean and they were able to explain how to find it.
Better still, it was only a small step to understanding the need to combine each person’s results and then share the total distance by the number of throws. With the context of the competition to hold on to, the whole class were able to make sense of why you add the numbers together and then divide.
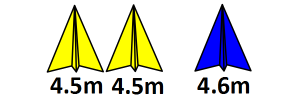
I’ve added one extra throw of the yellow plane. Who wins now? How did you decide?
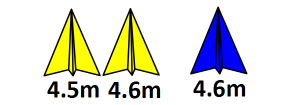
What if the second yellow throw changes? Who wins now? How did you decide?
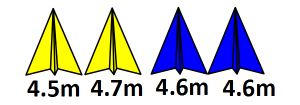
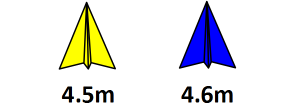
I’ve added a second blue plane and one of the yellow throws has changed. Who wins now? How did you decide?
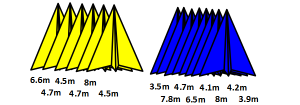
I’ve added a few yellow and blue planes. Who wins now? How did you decide?
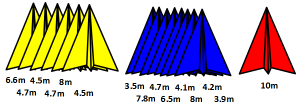
I’ve introduced a third plane that is only thrown once. Who wins now? How did you decide?
Resources
Paper Aeroplane Template
Paper Aeroplane Flipchart
Thanks
I didn’t make the video tutorial or the template. If it was you, thank you! Please step forward so that I can credit you properly. 🙂
Thanks for the amazing idea! I love your discussion of determining a winner.