The multiple personalities of fractions
The following is an extract of the text I wrote for an ebook aimed as a guide for first year TeachFirst maths teachers. The excerpt covers what I see as the major difficulty of grasping fractions – their multiple personalities.
You know where you are with integers. The number one means one and nothing else. It behaves like a one in every context. Two is the same – it was born to be a two. Same with three and four and five and any whole number.
That’s not the case with fractions. Fractions come in different forms, they mean different things in different contexts, and they obey different rules most of which aren’t intuitively obvious. The multiple personalities create a minefield for most adults, let alone pupils, and to make it worse there are multiple ‘multiple personalities’. Let’s take a look at the four sets of multiple personalities.
- What is the fraction trying to tell you? What does it stand for?
Fractions have three meanings.- Fractions can represent a position on a number line
This is the most overlooked personality in the maths classroom but it’s absolutely essential to understand that fractions hold a value in the way that whole numbers do. Fractions aren’t simply parts of a whole, they lie on a number line between all the integers. We can order fractions and we can compare their size because of this personality.Three quarters sits on this line between 0 and 1. We can see it’s closer to 1 and that it’s more than ½.
- Fractions are operations
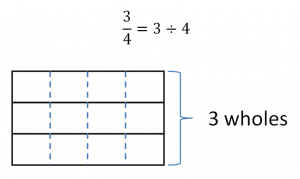
Let’s take ¾ again. At first glance, you might read that as “3 parts out of 4” but it can also be thought of as “three divided by four”. Fractions can be shorthand for division. - Fractions are parts of a whole
This is the obvious one, the one we start teaching, so we’ve left it until last.
Here’s the archetypal image to represent three quarters.

- Fractions can represent a position on a number line
- Every fraction has an infinite number of equivalent fractions but only one in simplest form
The idea that two fractions can be worth the same but involve different numerals is utterly perplexing. What happened to one being one and two being two? To find out that three quarters is equivalent to fifteen twentieths or 51/68 shakes the foundation of a pupil’s theory of number and can be quite unsettling, not to say confusing. - Improper fractions can be written as mixed numbers and mixed numbers can be written as improper fractions.
Fractions with a value greater than one have two separate forms – mixed number and improper fractions – before we even mention equivalence. Allowing for the possibility of a fraction where the numerator is bigger than the denominator, which is a mental leap in itself for those trained to see fractions as parts of a single whole (“What does 4 out of 3 mean?”), when you start dropping in mixed numbers, the perplexity needle enters the ‘dangerously high levels’ zone.Here are some questions and representations to use for helping pupils understand what improper fractions and mixed numbers are and how to convert between them.
- Fractions, decimals, percentages and ratio
You can tell by now where this is heading. That fractions can be written as decimals and percentages adds yet another layer to the cake of confusion. Take, for example, one tenth. We know that it can be written as 1/10, 0.1 or 10% and pupils can recognise that quickly too. They’re likely to draw false conclusions as to how convert between fractions and decimals from this, however, so when you tell them that 1/5 is not 5% and 20% is not 1/20 you’re really going to have some explaining to do.And then there’s the cousin of fractions – ratio – to contend with. How is that a ratio of 1:5 leads to a fraction of 1/6 or 5/6? When is a fraction a fraction and when is it a proportion?
Fractions are treacherous territory for students but that’s not to say you can’t teach it well. As with all of the tricky concepts in maths, you need to believe you can deliver. Enter the classroom with extra relish on the days you’re teaching fractions.
The rest of the chapter goes on to talk about specific teaching strategies for fractions. The full ebook, which includes the writers’ collective experience of teaching the 30 must-know maths topics, is available to download to your Kindle (or anything with the Kindle app installed). Simply search for ‘Teach First maths’ or visit this Amazon page.
Important note: While I contributed to the editing of How to Start on Teach First: Maths and writing some of the chapters, such as the one above, money from the sales doesn’t come to me. Money from sales goes to the educational charity Teach First, and its reinvestment in this collection of books for new teachers is at the discretion of the charity.
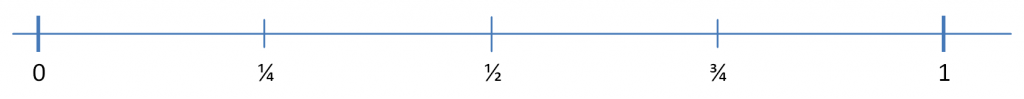




My faculty has found this extremely helpful as we look at our pedagogy of fractions. A couple of feedback points: we think it needs to include a fraction as part of a set of items rather than just parts of a whole, we would also include the word ‘equal’ in part B, 3 parts out of four EQUAL parts to always reinforce this idea to pupils.