Design your own mastery curriculum in maths
There seems to be a current surge from Heads of Maths and KS3 Maths Coordinators looking to adopt more of a mastery approach to teaching maths. This post is a quick run through of the journey the curriculum at King Solomon Academy has gone through and concludes with some advice for designing a maths mastery curriculum of your own.
Confession: We got it wrong to start with
The first maths curriculum we designed at King Solomon Academy didn’t work – at the end of year 7 our students hadn’t learned what we’d taught them.
That summer (2010), we went away wondering what we’d done wrong and came to appreciate the following flaws in the original curriculum:
- Flaw #1 – There’s so much to learn that we have to keep moving on. It turns out you don’t have to keep moving on – not at the expense of pupils actually learning what you’re trying to teach them. Yes, there’s plenty for them to learn but we don’t need to cram so many concepts into one year.
- Flaw #2 – They might not get it now but we’ll come back and teach it again in year 8 and 9 and *then* they’ll get it. We falsely reassure ourselves that they’ll understand it next time, however, the chances are they won’t. Why? Because if they didn’t understand it this time round, they probably don’t have the underlying skills they need to access what you’re teaching them and you probably don’t have time now to re-teach this for very long before you have to move on to the next topic. The tragedy is that year on year we keep piling on more things and we get to year 11 with a massive maths deficit.
- Flaw #3 – This is the way most other maths departments and publishers organise their curriculum so they *must* be right, with all their years of experience. Obviously a broken argument if they’re not right after all.
In short, we were moving the topic on too quickly (roughly every two weeks) and we were teaching “over” an insecure understanding of place value and poor recall of the basic number facts. We didn’t give our pupils a fair chance at learning when these factors were stacked against them.
What we moved away from
Here’s a snapshot of a year 7 curriculum that someone sent us recently, very very similar to the one that we started with 5 years ago:

With the experience the last 4 years has given us, these are our observations:
- No real time is given to the 4 operations or place value. It’s critical to spend 7-13 weeks on place value and the 4 operations unless you’re teaching a whole yeargroup of level 5s and above.
- Not enough time is spent on fractions (needs 6 weeks) or on algebra basics (needs 5 weeks)
- Area and perimeter are being taught together (should be as separate as possible)
- Mean, median and mode are being taught together (should be as separate as possible)
- Reflection, rotation and translation are being taught together (should be as separate as possible)
- The following don’t need to be taught at all – tessellations, function mapping
- The following don’t need to be taught in year 7: ratio, probability, transformations, functions and graphs, sequences, units of measurement, describing data, comparing sets of data
- Algebra comes up too soon in the year – save it until half-term 5
- Generally it’s trying to cover too much in too little time or in the wrong order (e.g. probability comes before fractions, although we’ve suggested probability doesn’t even need to appear in year 7) or together with concepts that are minimally different and likely to get confused (area/perimeter, mean/median/mode, reflection/rotation/translation).
- Too much chopping and changing doesn’t allow the pupils to get a footing in any of the topics before they’ve moved on, especially in schools that only have 3 hours a week of maths.
(Note: We were also sent a detailed breakdown of the curriculum, which is why we’re able to refer to things like tessellation and transformation that don’t appear on the overview.)
What we moved to
This is a snapshot of the King Solomon Academy KS3 curriculum: 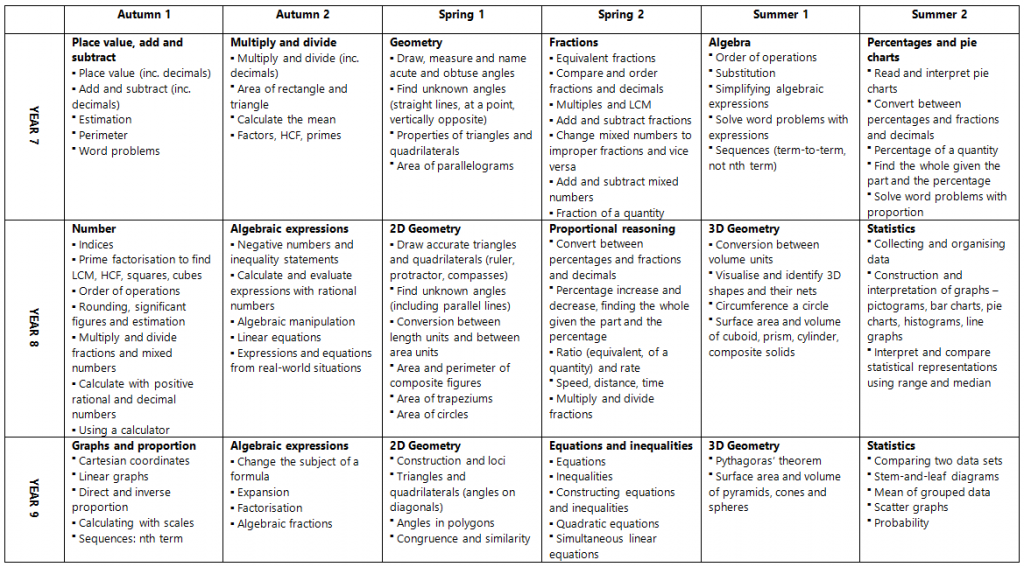
You should notice that more time is given to number work at the beginning of year 7 (especially times tables), we spend one half-term at a time teaching a topic rather than 2 weeks, some things are ‘missing’ (because they’re taught in KS4), we’ve tried to separate minimally different concepts and we’ve thought carefully about the order things are taught in so that all the while we’re building on top of prior learning.
Something to suggest it’s working
The graph shows the mean maths grade of our first three yreargroups over the last few years.
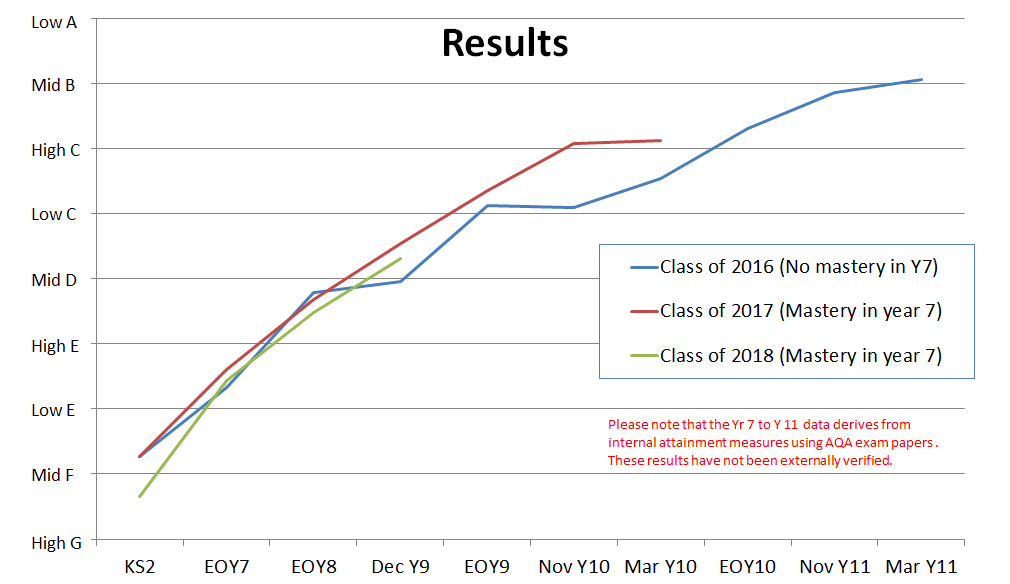
Notes: Exams were written by AQA especially for ARK schools using the Mathematics Mastery curriculum and the KS4 exams are past papers from AQA. We’ve ‘converted’ NC levels into GCSE grades. The conversion was crude but was applied to all datapoints in the same way and seems to have produced a reasonably smooth trajectory between the end of year 9 and beginning of year 10, which is obviously when the switch from NC levels to GCSE grades happens.
The simple messages from this are:
- The Class of 2016 (current year 11s) and the Class of 2017 (current year 10s) started from the same baseline. The Class of 2017 have had a higher average grade since the end of year 7, which could be attributed to the introduction of daily times tables practice and a switch to a mastery curriculum.
- Of the three yeargroups, the Class of 2018 had the lowest KS2 average but closed the gap by the end of year 7.
For the ResearchEd crowd, we realise the sample size is small, there is no control group and that we have no external results to validate any of this.
Six tips for creating your own maths mastery curriculum
- Don’t be afraid to go back to basics for 12 weeks in year 7 – more place value, more number bonds and single digit addition, more explicit teaching of mental arithmetic, more times tables, more written algorithms.
- Don’t be afraid to do *lots* of practice no matter what the discovery brigade tell you.
- Separate minimally different concepts so that things like mean, median and mode are not taught at the same time.
- Keep skills ticking along by dropping things from earlier in the year into starters, homework, flash tests and end of term exams.
- Don’t teach things until the pupils are ready to learn them, so, for example, don’t teach fractions until they can find factors and multiples, don’t teach factors and multiples (at the same time, ever) until they know the times tables.
- Spend more time teaching fewer things. For example, algebra can wait until the end of year 7, ratio can wait until year 8, probability and transformations can until KS4.
Credits
Far from building the curriculum in isolation, my wonderful colleagues at King Solomon Academy, at Mathematics Mastery (Helen Drury, especially) and from other schools in the ARK network have refined, contributed and altered different parts of the curriculum over the years. The snapshot presented above is something that many people have worked on and credit goes to them.
Disclaimers
School contexts are different, we get that. So while what we’ve said has suited our school, we’m not saying it suits everyone else’s.
We didn’t set out to call it a mastery curriculum or Singapore maths but somehow over the years the labels have stuck.
Related links
How we achieved dramatically good GCSE results in the poorest ward in London
Hi Bruno,
I have felt I should teach certain related things (area and perimeter, mean, mode, median etc) well apart for many years. Each time I have tried I have noticed no difference, however the class moves on out another teacher the following year so long-term retention is difficult to quantify. Given that I’m at ResearchED next week, is there any evidence we should keep these things well apart? I’m heavily a context-rooted teacher, and it’s difficult to separate some things.
Thanks for the comment. I’ve not delved into research on this. I always find that the pupils whose brains are working over-time in maths (various reasons why that would be), don’t separate the language and concepts easily. We rarely spend long enough making the concept 100% understood before teaching the algorithms so pupils try to learn “perimeter – add, area – multiply” and get confused when they’re taught so closely together. Thoughts?
Hi Bruno,
Thanks for sharing this, it’s definitely made me think about our own scheme of work. The idea of separating the similar topics, such as area and perimeter is new one to me and my concern is that, on the face of it, the students wouldn’t have to do much thinking to get the right answers. “In half term 1 we’re always adding, so add the numbers and the teacher will be happy” is a response I’d worry about. Doesn’t it fly in the face of the Thinking Skills approach where you focus on students having to decide for themselves when to add and when to multiply, or do you cover this at a later time? Also when you assess them throughout do they have to make these decisions, or do you limit content to that covered in the previous half term?
Really interested in your thoughts on this.
Kind regards,
Mike
Hi Mike,
Thanks for the comment. I’d never let students get away with misconceptions and so I’m always on the lookout for how my teaching might inadvertently foster them. I share your concern that on the face of it, pupils may not have to make decisions. However, I make it my business that they understand and can explain why they’re adding to find the perimeter. I’m sure everyone does this but I found that by introducing area to soon afterwards, they began overlapping the concepts and would forget the why and the how of finding the perimeter. I use a collapsible tent pole to model the concept of perimeter* and we look at the derivation of the word, splitting it into ‘peri’ and ‘meter’.
Of course, there’s more to perimeter problems than simply adding and I always look for a variety of problems that present the concept from different angles. It could be a missing side (rather than the perimeter), efficient perimeter calculations, comparing the perimeter of pentominoes, etc. There’s usually some decision making going on even if they know that at the heart of it there will be some addition and subtraction.
The decision you’re talking about does come up, please be assured, once area has been taught and understood.
On the matter of assessments, the pre- and post-tests each half-term are based on what we’re about to cover (in the case of the pre-tests) and have just covered (post-tests). Once a term there is a broader test on the maths they’ve studied over the last 12 months.
Come back with more questions as needed.
Kind regards,
Bruno
* Start with the tent pole fully extended into a straight line. They all know how to find the distance of a straight line. Then collapse it in 3 places to form a rectangle and discuss how you might go about finding the length around the outside (“peri” “meter”). The fact that the length of the original straight line has clearly been preserved helps them to quickly arrive at the need to add up the sides of the rectangle.
Thanks for this Bruno – it’s an interesting read. I completely agree that often schools try to fit so much content into each year group. I also don’t believe that ratio, functions and graphs, transformations, etc. all need to be taught in year 7. What I like about the Mastery curriculum is that students who need more time to internalize fundamental concepts have it, and students who can go off and investigate interesting aspects of a certain topic also get that time. One thing that I’ll take away from the post is your advice regarding basic number skills and the four operations. I personally was scared this year to spend time in class on that but it really is important. Of course, those who don’t need it can work on more interesting number connections but next year I’ll be adding in more lesson time for basic number skills and quick recall for those that need it.
Hi Bruno,
This is a very interesting read and definitely answers some questions that have come up in my mind about how a mastery curriculum is structured. It definitely seems to be a more thought out structure than the first model you present (again, similar to what we currently use) of covering everything once in a year, rushing through and leaving some kids behind or with insecure knowledge; and repeating for four more years!
Seeing this though means a couple more questions have cropped up. I’m interested to know the rationale for teaching circumference of a circle when you do (after area). I understand and definitely appreciate separating minimally different concepts, just wondering if there was any particular reason for this order.
Also, regarding the Class of 2016, did you start them on a mastery curriculum at the start of Y8? If so did you start them at the point where you’d start Y7s, or just miss out Y7 and go to straight to Y8, and has this had an effect?
Once again, thank you!
Alan
Thanks Alan.
On area of circles before circumference, area is taught in a half-term when area of other shapes is also being taught and there are some interesting composite shapes you can make with circles and parts of circles. Circumference is needed to calculate the surface area of a cylinder so it’s taught just before that.
Good question re Class of 2016 – yes, from year 8 we switched to a mastery curriculum. I dread to think how big the gap would have got if they’d spent 5 years on a non-mastery curriculum. Anyhow, the curriculum they received in year 8 was a hybrid of what we have now with the gaps from year 7 being filled in. Some things spilled over in to year 9 as well. So as the years have gone, the year 8 and 9 curricula have settled down. The big difference between Class of 2016 and Class of 2017 now is mental arithmetic. I regret not coming up with TT Rock Stars and bringing in rolling numbers while they were in year 7. The emphasis on learning the tables that I placed on Classes of 2017 onwards has made a big difference on cognitive load and ultimately on accessing all the things that sit on top of multiplication and division.
Fractions
2/7 add 3/8
Multiply 7 and 8 ……Common denominator 56
56 divided by 7 = 8…. Multiplied by 2 = 16
56 divided by 8 = 7 …..Multiplied by 3 = 21
Add 16 and 21 = 37/56.
Think how many times tables and related division facts needed to be recalled. With instant recall of these facts, students can concentrate on understanding the calculation of the fractions rather than using their mind to work out the answer to the facts.
Do the same for percentages, algebra, area/perimeter.
1. If students don’t have instant recall of times tables and related division facts, how do they follow any fractions, percentages, algebra and area/perimeter teaching?
2. Is there any point teaching any of the above until students have instant recall of TTs and RDFs?
3. Wouldn’t it be better to teach instant recall of TTs and RDFs, then all of the above in question 1 could be taught and understood in a matter of a few lessons where everyone in the understood?
Helen Maden
You’re preaching to the converted on this one!
I teach Year 5/6 and don’t have a single pupil who does not have instant recall of their tables. I always spend the whole of the Autumn Term doing number bonds, tables and related division facts plus written calculations ….that’s it. I panic a bit in the Spring Term as I have to literally pack everything (i.e. all that is on the King Solomon Academy new Year 7 curriculum and much of what is on the Year 8 curriculum) into a few weeks in time for SATs – children pick up brand new concepts quickly and generally make 4 or 5 sub-levels progress. It sounds mad but it works.
Last Year I had 17 children in Y6
1 level 4b (child only 1a at the end of Y2)
8 level 5
8 level 6
It is interesting that the new curriculum for maths for primary indicates that children need to know their tables by the end of Y4 – is that going to happen? – From 2016, there is now NO assessment in SATs for recall of tables/division facts. In the present mental maths test there are always a couple of questions on recall of TT and RDFs.
What else is it essential for children coming from Primary School into Secondary School need to be able to do in order to make good progress?
I too teach years 5/6. For the last 12+ years I have, each year, had a group of approx 22 children levelled 2a-3a. After 2 terms the 2a are 4c and the 3a are 4a/5c. My first term is simply focused on times tables, no.bonds and the four rules and their application to everyday problems. I still panic a little with everything I am left to do before sats, but we always fly through. I have been criticized for my ideas but left alone as no one can deny the results and certainly no one wants them to stop! I have now realised what I have been doing has a name and boy, am I going to share it! It is all about giving confidence to those kids who for all their maths education have never been able to understand anything because the teacher feels they have to do a new topic every week/fortnight. I have a name for it- yahoo-there’ll be no stopping me now! x
Good for you! There are not many of us that are allowed to equip children with the knowledge and understanding they need. Most school leaders focus on monitoring lessons and scrutinising children’s books to check teachers are covering the ridiculously wide primary maths curriculum (which from September is going to get even wider).
Helen x
I really love what you’re doing here. Thank you for sharing.
I would love to implement a similar scheme, but I’m wondering;
Do you find it a problem that all pupils start at the same point? Do some more able pupils move through more quickly or do you stick to the scheme regardless of pupil ability – can they show ‘mastery’ early?
Please keep us informed of how things are going.
Chris
Good questions Chris – ones that I had to wrestle with myself before adopting this approach. The ‘problem’ of everyone starting at the same point is very solvable – higher attainers go deeper into place value and have the opportunity to explore binary and dozenal number systems, as well as comparing abaci and sorobans and deciphering reading foreign and ancient numerals.
Can they show mastery early – yes, absolutely. With some topics some pupils arrive at mastery level. So for them it’s time to go deeper, not broader. As in, I wouldn’t start teaching them the next topic on the course.
To deal with the minefield of differentiation a mastery curriculum can create (especially in a mixed ability classroom), I started blending the learning – mixing how much I taught in the classroom with how much they learned online. See http://www.mrreddy.com/project24/index.htm
Hi Bruno. I have just discovered this blog and was interested in the ideas behind the mastery curriculum as that is what we are all expected to produce in Primary schools now. I am curious though as to why you feel algebra and ratio don’t need to be taught until late in year 7 or even in year 8. They are both concepts that are taught in years 5 and 6. If they then don’t revisit for over a year, it’s a long while for them to remember their previous learning.
Hi Jan,
Thanks for leaving a comment. You’re right these are taught at primary school, along with fractions, percentages, area, perimeter, mean, etc. Despite this we found, year after year, that the pupils were very insecure in these areas. Why? Because they were still insecure in the basics. Not much point in teaching ratio and algebra, even in year 5 & 6, if the foundations aren’t there.
So our curriculum changed to ensure the basics were mastered. Only at that point do we feel it’s safe to proceed with algebra. Ratio we save until year 8 because it’s pretty low priority by comparison to fractions, percentages and multiplicative reasoning.
Hope that all makes sense.
Bruno
Hi Bruno, great blog.
I teach in Y6 and I completely agree with you re: ratio/algebra. Unfortunately, the issue we have – particularly with any child who shows signs of daring to be Level 4 before Christmas in Y6 – is that we have to teach these things that the children are not “ready” for in order to get them “ready” for the Level 5 aspect of SATS. It’s madness; a complete waste of time. However, the new curriculum just moves these things even earlier – some of these concepts are now beginning to rear their heads in Y5 as the bar is raised. I think most Y5/6 teachers would wholeheartedly agree with what you’re saying – we’re spreading our teaching ‘butter’ too thin and not enough of this sticks to the ‘bread’ as learning – pardon the analogy!
Found your ideas really interesting, first time I’ve read your ideas but I’ve got you bookmarked now!
Hi Andy, thanks for taking the time to leave a comment. Great butter analogy!
On the assumption pupils can meet the new NC requirements, what do you think needs to change in the way we teach? In the way we design lessons, set out the curriculum, handle intervention, group pupils, etc.?
Concerning issues you raised in respnse to Andy’s comments:
Andy and Bruno,
The question is, “What is better for the child’s mathematical develeopment in the long run?”
What is it going to be best for (her) to learn and consolidate now so that (she) is best prepared to make the most progress in the remaining 5 years before she does GCSE Maths and so be prepared for the Maths she needs in life.
For your own performance management, your own schools’ data and in turn to get a good/outstanding ofsted, it would be to intensely teach tricks on a one-to-one basis or in a small intervention group – go through loads of past papers and explicitly ‘teach’ her how to get enough marks for a 4b. (Probably avoiding fractions, ratio and algebra questions that require a sound understanding of times tables), This is what most of good/outstanding Y6 teachers do!
What you should really do, is prepare the children for secondary school by making sure they have mastered these basic skills:
1. Can they instantly recall the 221 addition facts to 20 without counting on fingers and recall related subtraction facts ?
2. Do they instantly recall and understand times tables and related division facts?
3. Can they quickly and reliably perform written methods of the 4 operations with understanding?
In terms of the new curriculum, they should have come into Y5 (let alone Y6) being able to perform all 3 in order to ‘do well in National Curriculum Tests’.
When as Y6 teachers, on management’s demand, we push struggling Y6 children through to a 4b, we are saying to the rest of the teachers in the school is, “No problem – you have fun in maths, forget about the progress of the basic skills for those who are struggling and we will make sure all children in this school make the ‘progress’ In Y6!”
The struggling children get a 4b but aren’t really a Level 4 at all. So in Y7, teachers are asking, “How on earth did this child get a Level 4?”. The answer is the same as when employers ask, “How did this 16 year old get C in maths at GCSE?”. When we get annoyed by this question, we should ask ourselves, “Would she get a Level 4b or get a C at GCSE if we left them over the summer, and they did the exam in September?”
The long term answer is to make sure that children have mastered the basic skills by the time they leave Y4. If they are not mastering these skills – you should be asking, “Why not?” so you are not worrying about a child ‘getting a Level 4b’ with only 22 days to go before the Year 6 Paper A.
For future children in the school, don’t be inadvertently saying to the rest of the staff, “Leave progress to me!” Put some of your energy into helping the Head/Maths Co-ordinatior make sure there are systems in place for children to master the basic skills before they get to Y6. It will be hard to begin and take years to feel the difference with but will pay off in the end – and you will never be in this position again – it’s horrible.
It’s not good for your health!
It’s not fair on the child.
The only positive for a child struggling at Maths going through intervention to get a Level 4, is that they don’t feel like a Level 3 failure. The negatives are that there has been a total waste of time in maths during their last 6 months at primary school and they will struggle at secondary school as they still don’t have the basic skills.
I have 30 Y5/6 children – 18 Year 6s. I did have this problem – but don’t anymore – except when children come to us from other schools. At the moment I am happily teaching fractions, percentages, decimals ratios and algebra to Y5/6 and they love it (only because they have already mastered the basic skills).
This is because there is a now firm focus on basic skills in Y3 and Y4 – especially for those children who are beginning to struggle – not just for those who quickly grasp it.
Helen
Hi Bruno
I’m a new convert to mastery but have my department behind me – just trying to convince the powers that be that it is the way to go. In light of the new GCSE specifications, I’ve started on a 5 year mastery scheme (based initially on your KS3 one on the website). One SoW for every student in the school – sounds too good to be true. Was going to put the core content at the front and higher at the end. Tier of entry will be determined by how far the students have progressed through the units. Just wondered if anyone was doing something similar or if people used different things for KS3 and 4
I think that I am in a similar situation to that which you have outlined above. Have text books been a considered element to your implementation? If so, how did you go about auditing against mastery criteria?
Hi Darragh,
The NCETM are currently doing some work on what makes a good textbook and have audited ones against a mastery approach. The ones that fit the bill the best are: My Pals Are Here and Maths No Problem. Both of these are Singapore titles but there is work underway to Anglicise them. Don’t expect much during this school year. The original Singapore books are worth a look if you can get them for a good price.
Thanks,
Bruno
Fantastic idea, and we are starting incorporate a lot of this thinking into designing our new KS3 scheme of work. However, have you thought about anything similar for the GCSE? It is looking more and more likely that we are going to spread the GCSE content over 5 years, which is essentially what this is already doing, but do you have a route plan for years 10 and 11?
Hi Steve,
Many thanks for the message. We apply the same principles to KS4, in that we spend longer on topics (about 4 weeks – not as long as in KS3), use direct instruction, daily homework, separation of some content. However, we find that the students are able to take on new content at a faster rate, having got a firm grounding in KS3. There is an expectation on the pupils that they work harder and pick up more things more quickly now.
Some of the key teaching methods we still use include: minimally different examples, mastering each step of each problem type, trickle feeding past content and working the problem backwards (probably titles of future blog posts).
The other evening a forum was set up for people to share their questions and help one another with answers related to the development of their mastery curriculum. Perhaps you’d like to check one of the threads on the forum as several people are asking the same thing.
Link to mastery maths forum. Or you can click on the button in the menu above.
When our KS4 curriculum is tidied up, I’ll share it. It’s not really in a format I’m ready to send out!
Thanks,
Bruno
Hello Mr Reddy,
I’ve really enjoyed reading this. I’m an English specialist who is looking after a maths department until we appoint a head of maths, which could feasibly be September. I’m enjoying the role, (I did enjoy maths at school) and this approach just makes so much sense to me as an ‘outsider’ who is finding the ‘running the gauntlet’ approach through all those topics mind boggling!
This model is the way I want us to move forward but how do I begin to implement something like this in Y8 and Y9 where the learners DON’T have a solid foundation in number. How do I begin to pull this back?
Any advice greatly appreciated!
Sam Twigg
Hi Sam,
Thanks for the comment. Great question.
It’s not easy is the answer. Any shift in approach mid-way through a course is going to require some compromises. If you were going to carry forward any of my suggested year 7 content in year 8, it would be place value, the 4 operations and fractions. Similarly, for year 8 content in year 9, I would make sure year 9 teachers focused on negative numbers (see here) and angle facts, as well as all the other things. Like I said, there are going to be some compromises in terms of how much time you’ll be able to spend on each concept if you’re loading in even more.
Happy to chat on the phone some time during the rest of the half-term holiday (or beyond) if that helps. Just email bruno@mrreddy.com
Cheers,
Bruno
Hi Bruno,
Thanks for sharing your overview. The more I read blogs on this approach the more I wonder why we haven’t been doing this before. It just makes so much sense. I have managed (I think) to convince my department it is the way forward (despite the ease of buying in a scheme of work). Could you clarify the content in the place value unit please? Am I right in thinking it involves negative numbers, rounding to decimal places and multiplying and dividing by powers of 10?
Thanks in advance.
Nicke
Hi Nicke,
Thanks for leaving a comment – I’m glad it makes sense.
Place value in year 7 contains simply being able to read and write numbers large numbers up to 1 billion and small numbers down to 1 thousandth. They need to know the names of the place value columns, their order and the value of any digit in the number. Rounding comes up that half-term at the same time as estimation (rather than with place value). Negative numbers are saved for year 8.
The idea that place value columns are a power of 10 apart is represented informally when we play with the abacuses (?) but the procedure of x10 and /10 is not practised until the next half-term.
Hope that makes sense but by all means ask more questions to clarify.
Cheers,
Bruno
Thanks for this Bruno, I appreciate you giving up your time. How long would you spend on place value? I like the idea of playing with an abacus but not sure we have anywhere near enough. Do you use concrete resources a lot? Which ones would you recommend the most? Also where would you teach finding the midpoint of two numbers?
Thanks again
Nicke
Hi Bruno,
My school is in the process of adapting a mastery approach and while I love the idea of it I am struggling to see how it will work in practice. We are trying to encourage the pupils to develop understanding of topics by spending more time on each one, but how does this split into lessons? I think I am so used to ‘traditional’ schemes of work that are quite prescriptive so I am finding it difficult when only given a module title and some bullet points.
For example, in your Year 7 Autumn 2 you cover: multiplication and division, area of a rectangle and triangle, mean, factors, HCF and primes. How do you cover these in 6/7 weeks? I would normally spend perhaps 4 weeks on this, how do you split this into lessons?
My school is in the middle quite a big over hall; new headteacher, new Head of Maths, a lot of new members of the department amongst others. With so much going on I’m starting to become a bit of a stress head at the moment, so any help would be appreciated!
I am moving to a new school in September that is following this scheme of work. I have not had any CPD relating to mastery teaching and so am worried that I will not be able to use the scheme of work effectively. Can I ask:
a) How many hours of teaching does this represent? We have 28 hours per half term for year 7.
b) How do you assess students that are targeted a grade 3 at the end of year 7, when there are little to no topics that are at grade 3?
c) How much of an influence has the new KS2 specification had where they are now taught more formal methods, mastery in Primary schools and bar modelling techniques?
Any help greatly appreciated.